Le module Matplotlib#

Vidéo: Afficher des courbes#

Afficher des points#

Les représentations graphiques sont très importantes en science, à la fois pour la compréhension et l’interprétation d’un problème. Pour cela nous allons utiliser le module Matplotlib.

La fonction plot() du module pyplot de Matplotlib permet d’afficher des points sur un graphique à 2 dimensions. Pour cela il faut donner comme arguments à la fonction plot() :

  • argument 1 : liste des abscisses des points à afficher (x)

  • argument 2 : liste des ordonnées des points à afficher (y)

# Importation du module pyplot de Matplotlib, renommé plt
import matplotlib.pyplot as plt

# Listes des coordonnées des points à afficher
x = [2, -9, -5, 6, 1] # Abscisses
y = [6, -3, 6, 0, -6] # Ordonnées

# Graphique
plt.plot(x, y)
plt.show()
../../../_images/af95c3454c10effc5fc1c52b27cd17c0ac34033b600b5d9aa89e5b302cecf343.png

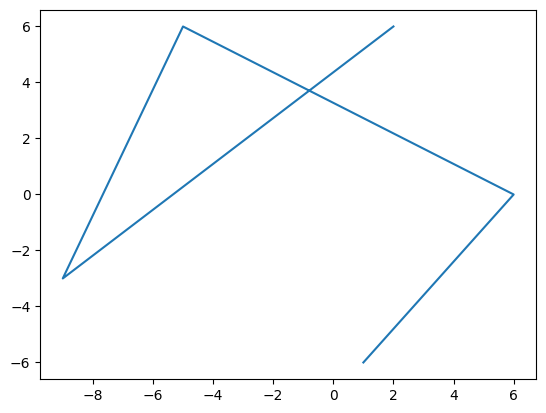
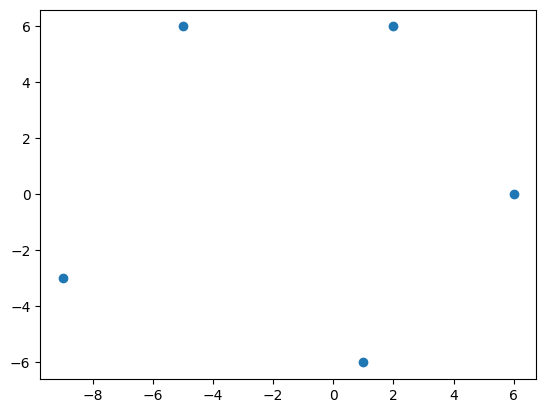
Par défaut, la fonction plot() relie chaque point par une droite. Cependant, il est possible d’afficher seulement les points avec :

plt.plot(x, y, 'o')
plt.show()
../../../_images/45da31eacba56b9ae2e9e2023904b9d2144e70920d1b95cf7127bfcc559337c6.png

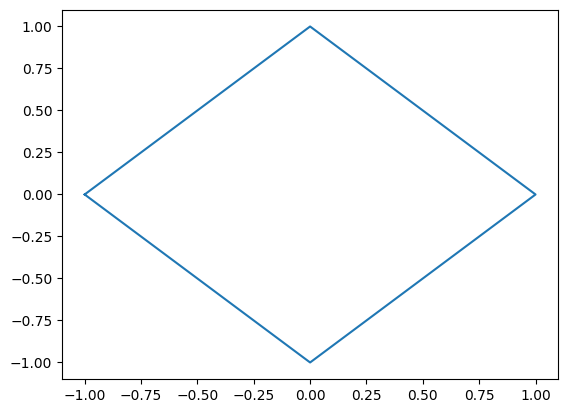
Exercice#

Dessiner un losange grâce à la fonction plot(). Pour cela, il faut déterminer les coordonnées des coins du losange.

Hide code cell source 
# Dessiner un losange
x = [-1, 0, 1, 0, -1]
y = [0, -1, 0, 1,  0]
plt.plot(x, y)
plt.show()
../../../_images/3d57753727dcaab03da03eb73c1e687f95057cbcf10efb98490f6809a006c808.png

Représentation graphique d’une fonction mathématique#

Pour une fonction réelle d’une variable réelle \(f:\mathbb{R}\rightarrow\mathbb{R}\), l’ensemble des points de coordonnées \((x,f(x))\) définit le graphe de la fonction \(f\). Ce graphe est contenu dans le plan \(\mathbb{R}^2\) et se présente sous la forme d’une courbe appelée courbe représentative. Nous allons tracer cette courbe représentative à l’aide de Matplotlib.

Cependant la courbe représentative contient une infinité de points (courbe continue), alors que Matplotlib nous permet seulement d’afficher un nombre fini de points. Il faut alors discrétiser cette courbe, c’est-à-dire choisir un nombre fini de points pour la représenter. Voici un exemple avec la fonction sinus :

# Importation du module Numpy
import numpy as np

# Choix de l'intervalle de représentation
intervalle_min = 0
intervalle_max = 10 * np.pi

# Choix du pas de discrétisation
pas = 0.1

# Calcul du nombre de points
intervalle = intervalle_max - intervalle_min
num_points = int(intervalle / pas) + 1

# Création du tableau contenant les abscisses des points
x = np.linspace(intervalle_min, intervalle_max, num_points)

# Création du tableau contenant l'image du tableau x par la fonction sinus
y = np.sin(x)

# Courbe représentative
plt.plot(x, y)
plt.show()
../../../_images/a96669b575d4c99a489d4762692763b8acb0b08088937a354410e16c3b5696ac.png

Comme on a choisi un pas petit devant la période de la fonction sinus, on a l’illusion d’avoir tracé une courbe continue. Cependant, ce n’est qu’un nombre fini de points reliés par des droites. On peut s’en persuader en traçant les points sans les relier :

plt.plot(x, y, '.')
plt.show()
../../../_images/4fb667fb6d4aac39742d17113c9dc986d8b024352254855bc52a9c9bf49bb1f4.png

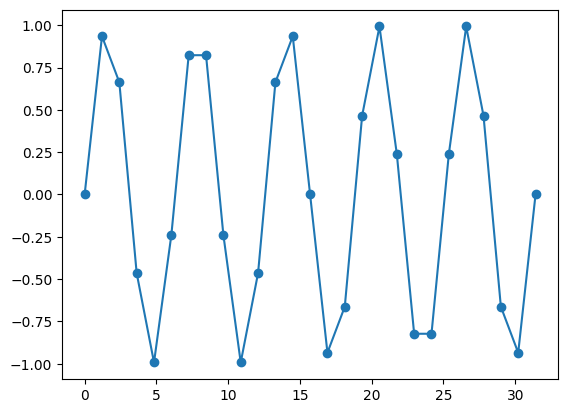
Ainsi, si le pas de discrétisation n’est pas adapté, la représentation de la courbe sera mauvaise. Par exemple, un pas de 1.2 ne permet par de bien représenter la fonction sinus :

# Choix du pas de discrétisation
pas = 1.2

# Calcul du nombre de points
intervalle = intervalle_max - intervalle_min
num_points = int(intervalle / pas) + 1

# Création du tableau contenant les abscisses des points
x = np.linspace(intervalle_min, intervalle_max, num_points)

# Création du tableau contenant l'image du tableau x par la fonction sinus
y = np.sin(x)

# Courbe représentative
plt.plot(x, y, '-o')
plt.show()
../../../_images/4d3d0954ed645fdfa26e8dbe74bab519a1a8db73c3cf8c1f980b0f8e4539181d.png

Exercice#

Représenter graphiquement la fonction tangente hyperbolique en choisissant un intervalle et un pas de discrétisation appropriés. La fonction se nomme tanh() dans le module Numpy.

Hide code cell source 
# Choix de l'intervalle de représentation
intervalle_min = -5
intervalle_max = 5

# Choix du pas de discrétisation
pas = 0.1

# Calcul du nombre de points
intervalle = intervalle_max - intervalle_min
num_points = int(intervalle / pas) + 1

# Création du tableau contenant les abscisses des points
x = np.linspace(intervalle_min, intervalle_max, num_points)

# Création du tableau contenant l'image du tableau x par la fonction tanh
y = np.tanh(x)

# Courbe représentative
plt.plot(x, y)
plt.show()
../../../_images/bcddbb3c241ae675d1b6b827e4b8da9bf2dedea1f818e49004e7b26fa6f6d83c.png

Vidéo: Mise en forme#

Représentation de données#

Il est bien sûr possible de représenter graphiquement des données. Généralement les données sont écrites dans un fichier ou sous la forme d’un tableau. Par exemple, prenons l’évolution de la population mondiale telle que donnée sur la page Wikipédia sous forme d’un tableau :

Année

Population

1950

2536431

1955

2773020

1960

3034950

1965

3339584

1970

3700437

1975

4079480

1980

4458003

1985

4870922

1990

5327231

1995

5744213

2000

6143494

2005

6541907

2010

6956824

2015

7379797

2020

7794799

Nous avons vu que Matplotlib est compatible avec les tableaux Numpy. Créons les tableaux suivant :

  • en abscisse : l’année, avec le type datetime64

  • en ordonnée : la population, avec le type int64

# Création des tableaux
x = np.arange('1950', '2021', step = '5', dtype = 'datetime64[Y]')
y = np.array([2536431, 2773020, 3034950, 3339584, 3700437, 4079480, 
              4458003, 4870922, 5327231, 5744213, 6143494, 6541907,
              6956824, 7379797, 7794799], dtype = 'int64')

# Représentation des données
plt.plot(x, y, 'o')
plt.show()
../../../_images/b5ea103d23036c354eaa74f6acdff916b1535895013ac0fc5436b50ec556a4ce.png

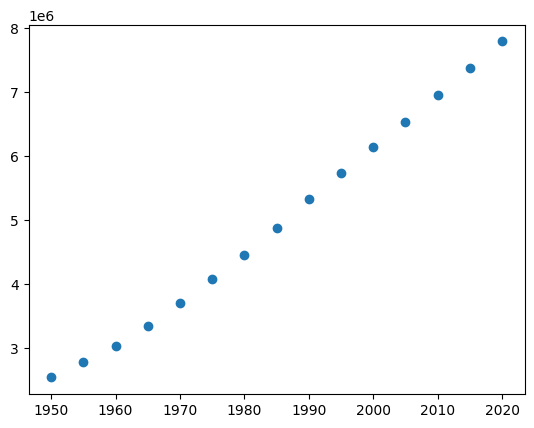
Cependant, il est d’usage d’ajouter des informations au graphe afin qu’une personne puisse correctement interpréter la signification des différentes données. Voici les commandes usuelles utilisées pour rendre un graphe plus lisible :

fonction

description

title()

titre du graphique

xlabel()

titre de l’axe des abscisses

ylabel()

titre de l’axe des ordonnées

grid()

affichage d’une grille de coordonnées

xlim(xmin, xmax)

limites de l’axe des abscisses

ylim(ymin, ymax)

limites de l’axe des ordonnées

Exercice#

Reprendre le graphe précédent et utiliser les commandes ci-dessus pour :

  • mettre un titre au graphe,

  • aux axes des abscisses et des ordonnées,

  • choisir l’intervalle pour l’abscisse entre 1950 et 2030,

  • pour l’ordonnée entre 0 et 10 milliards,

  • afficher une grille de coordonnées,

  • de plus, on affichera la population en milliards.

Note : pour créer un objet datetime64 il faut écrire np.datetime64('1950','Y')

Hide code cell source 
plt.plot(x, y / 1e6, 'o')
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (milliard)')
plt.xlim(np.datetime64('1950', 'Y'), np.datetime64('2030', 'Y'))
plt.ylim(0, 10)
plt.grid()
plt.show()
../../../_images/01f51c1f14d5d4c1a2f29dc97b0385bdd102d99fa37bc3fce1279bc875d6156c.png

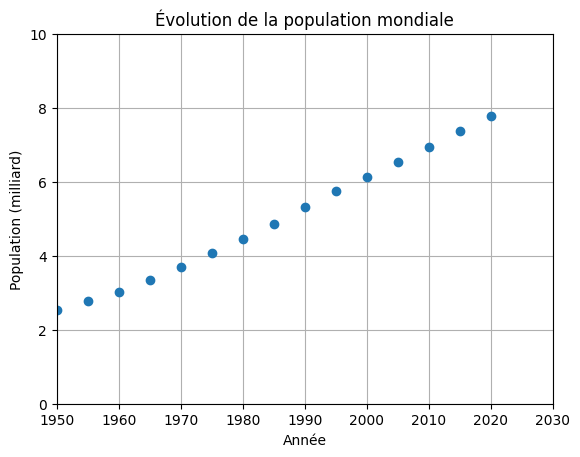
Afficher plusieurs courbes#

Il est très simple d’afficher plusieurs courbes sur le même graphe : il suffit d’appeler successivement la commande plot(), ou bien de mettre les tableaux à la suite dans la même fonction plot().

Prenons par exemple l’évolution de la population mondiale selon les calculs de l’Organisation des Nations Vnies (ONU) jusqu’à 2100. L’ONU définit 3 scénarios possibles, dont les chiffres sont donnés dans le tableau suivant :

Année

Variante basse

Variante moyenne

Variante haute

2020

7 794 779

7 794 799

7 794 799

2030

8 363 453

8 548 487

8 733 522

2040

8 716 310

9 198 847

9 682 332

2050

8 906 797

9 735 034

10 587 774

2060

8 882 880

10 151 470

11 529 222

2070

8 675 770

10 459 240

12 495 987

2080

8 331 397

10 673 904

13 478 079

2090

7 869 840

10 809 892

14 515 851

2100

7 322 116

10 875 394

15 600 369

Reprenons la courbe de l’évolution de la population entre 1950 et 2020, et ajoutons les différentes projections faites par l’ONU :

# Tableau des abscisses pour les projections
xp = np.arange('2020', '2101', step = '10', dtype = 'datetime64[Y]')

# Tableau des différentes projections
proj1 = np.array([7794779, 8363453, 8716310, 8906797, 8882880, 8675770, 8331397, 7869840, 7322116])
proj2 = np.array([7794799, 8548487, 9198847, 9735034, 10151470, 10459240, 10673904, 10809892, 10875394])
proj3 = np.array([7794799, 8733522, 9682332, 10587774, 11529222, 12495987, 13478079, 14515851, 15600369])

# Tracé des différentes courbes
plt.plot(x, y / 1e6, label = 'entre 1950 et 2020')
plt.plot(xp, proj1 / 1e6, label = 'variante basse')
plt.plot(xp, proj2 / 1e6, label = 'variante moyenne')
plt.plot(xp, proj3 / 1e6, label = 'variante haute')

# Titres et autres
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (milliard)')
plt.xlim(np.datetime64('1950', 'Y'), np.datetime64('2100', 'Y'))
plt.ylim(0, 16)
plt.grid()
plt.legend()
plt.show()
../../../_images/5b5e861d1a748e198b77757d04e16214defaa320b7618b2db797c30137b59bec.png

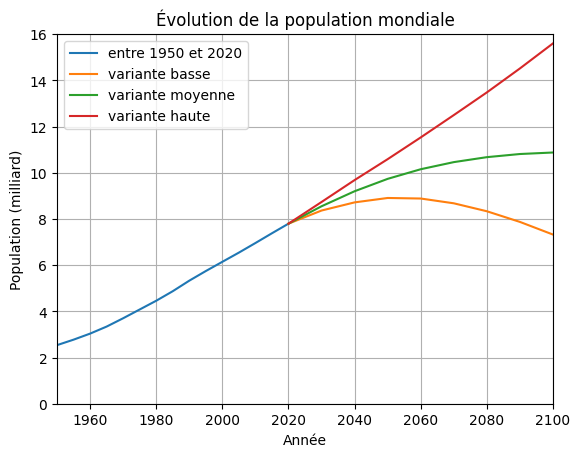
On a utilisé l’option label de la fonction plot() pour nommer chaque courbe, puis la fonction legend() afin d’afficher la légende. De manière alternative et plus compacte, on aurait pu écrire :

# Tracé des différentes courbes
plt.plot(x, y / 1e6, xp, proj1 / 1e6, xp, proj2 / 1e6, xp, proj3 / 1e6)

# Titres et autres
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (milliard)')
plt.xlim(np.datetime64('1950', 'Y'), np.datetime64('2100', 'Y'))
plt.ylim(0, 16)
plt.grid()
plt.legend(['entre 1950 et 2020', 'variante basse', 'variante moyenne', 'variante haute'])
plt.show()
../../../_images/5b5e861d1a748e198b77757d04e16214defaa320b7618b2db797c30137b59bec.png

Vidéo: Style des courbes#

Une question de style#

Plusieurs options de la fonction plot() sont utiles pour contrôler le style de la courbe représentée. Voici quelques options parmi les plus utilisées :

option

description

valeurs

color

couleur de la courbe

‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’

linewidth

épaisseur du trait

nombre réel

linestyle

style du trait

‘-’, ‘–’, ‘-.’, ‘:’

marker

style des points

‘+’, ‘*’, ‘,’, ‘.’, ‘1’, ‘2’, ‘3’, ‘4’, ‘<’, ‘>’

Reprenons la courbe précédente et traçons une courbe plus lisible et plus adaptée pour l’impression en noir et blanc :

# Tracé des différentes courbes
plt.plot(x, y / 1e6, label = 'entre 1950 et 2020',    color = 'k', linestyle = '-',  linewidth = 3)
plt.plot(xp, proj1 / 1e6, label = 'variante basse',   color = 'k', linestyle = '--', linewidth = 3)
plt.plot(xp, proj2 / 1e6, label = 'variante moyenne', color = 'k', linestyle = '-.', linewidth = 3)
plt.plot(xp, proj3 / 1e6, label = 'variante haute',   color = 'k', linestyle = ':',  linewidth = 3)

# Titres et autres
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (milliard)')
plt.xlim(np.datetime64('1950', 'Y'), np.datetime64('2100', 'Y'))
plt.ylim(0, 16)
plt.grid()
plt.legend()
plt.show()
../../../_images/caad946f24f80632e54b4fcae1a7ba023062281bbff8520b6f5241f30689cb04.png

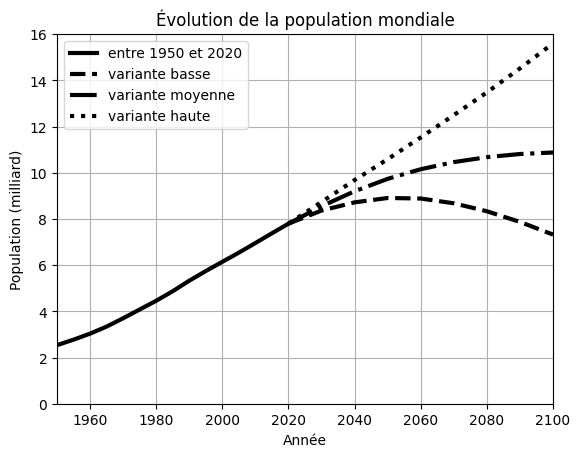
Exercice#

On donne une estimation de la population entre 1700 et 1950 :

Année

population (milliards)

1700

0,640

1750

0,655

1800

0,950

1850

1,270

1900

1,650

1910

1,750

1920

1,860

1930

2,07

1940

2,3

1950

2,5

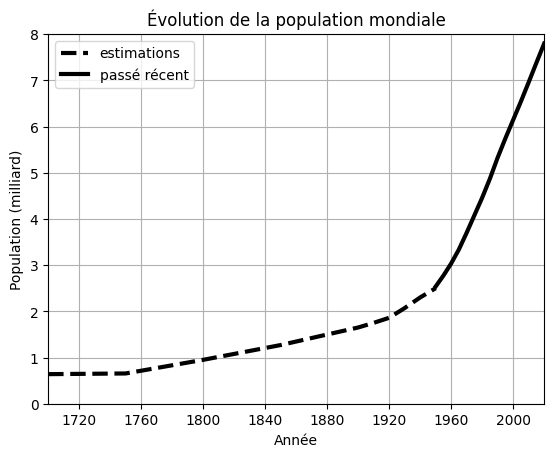
En reprenant les tableaux définis précédemment et en créant de nouveaux tableaux, tracer la population estimée entre 1700 et 1950, et la population récente entre 1950 et 2020, sur le même graphe. Mettre des titres et une légende.

Hide code cell source 
# Tableau des dates pour l'estimation
temps_estime1 = np.arange('1700', '1900', step = '50', dtype = 'datetime64[Y]')
temps_estime2 = np.arange('1900', '1951', step = '10', dtype = 'datetime64[Y]')
temps_estime = np.append(temps_estime1, temps_estime2)

# Population estimée
population_estimee = np.array([0.64, 0.655, 0.95, 1.27, 1.65, 1.75, 1.86, 2.07, 2.3, 2.5])

# Tracé des différentes courbes
plt.plot(temps_estime, population_estimee, label = 'estimations', color = 'k', linestyle = '--', linewidth = 3)
plt.plot(x, y / 1e6, label = 'passé récent',  color = 'k', linestyle = '-',  linewidth = 3)

# Titres et autres
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (milliard)')
plt.xlim(np.datetime64('1700', 'Y'), np.datetime64('2020', 'Y'))
plt.ylim(0, 8)
plt.grid()
plt.legend()
plt.show()
../../../_images/025316aa5ae1ccde306f8e98716f2082ddab32f2625183a2566790dbe5082833.png

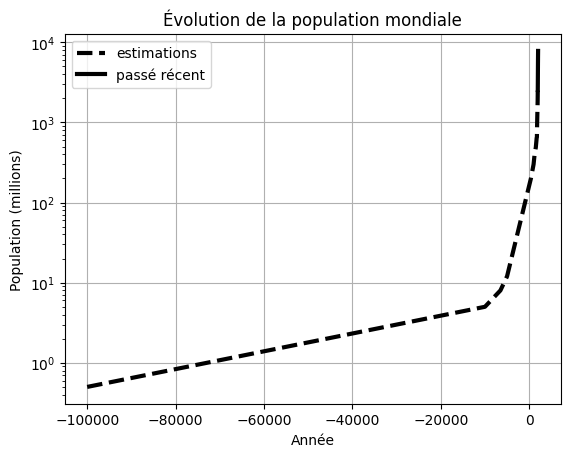
Échelle logarithmique#

Il arrive souvent que des quantités varient sur plusieurs ordres de grandeur. Il peut être pratique alors de tracer le graphe en échelle logarithmique. Voici les différentes fonctions qui permettent de tracer en échelle logarithmique :

fonction

description

loglog()

échelle log pour les deux axes

semilogx()

échelle log pour l’axe des abscisses

semilogy()

échelle log pour l’axe des ordonnées

Prenons par exemple l’évolution estimée de la population depuis l’année -100 000 jusqu’à 1950 :

Année

population (millions)

-100 000

0,5

-10 000

5

-6 500

8

-5 000

12

400

200

1000

300

1250

410

1500

485

1700

640

1750

655

1800

950

1850

1 270

1900

1 650

1910

1 750

1920

1 860

1930

2 070

1940

2 300

1950

2 500

Le type datetime64 ne peut pas être utilisé pour représenter des dates trop anciennes. Nous allons alors utiliser le type integer pour les tableaux de dates :

# Tableau des dates pour l'estimation
temps_estime1 = np.array([-100000, -10000, -6500, -5000, 400,
                  1000, 1250, 1500], dtype = 'int64')
temps_estime2 = np.arange(1700, 1900, step = 50, dtype = 'int64')
temps_estime3 = np.arange(1900, 1951, step = 10, dtype = 'int64')
temps_estime = np.concatenate((temps_estime1, temps_estime2, temps_estime3))

# Population estimée
population_estimee = np.array([5e-1, 5, 8, 12, 200, 300, 410, 485, 
                               640, 655, 950, 1270, 1650, 1750, 1860, 2070, 2300, 2500])

# Tracé des estimations
plt.semilogy(temps_estime, population_estimee, label = 'estimations', color = 'k', linestyle = '--', linewidth = 3)

# Tracé du passé récent
xint = x.astype(int) + 1970 # conversion de datetime64 vers integer
plt.semilogy(xint, y / 1e3, label = 'passé récent', color = 'k', linestyle = '-', linewidth=3)

# Titres et autres
plt.title('Évolution de la population mondiale')
plt.xlabel('Année')
plt.ylabel('Population (millions)')
#plt.xlim(-1e5, 2020)
#plt.ylim(1e-4, 10)
plt.grid()
plt.legend()
plt.show()
../../../_images/2ed3448b4526cc135282f175d78b60e61bf49987470b37598c01bcbb7e3ca986.png