Démarche de modélisation

Le but de ces exercices est d’appliquer le modèle de l’accéleration constante à 1D à de nouvelles situations, de complexifier le modèle et d’explorer ses limitations.

Pile ou face

On joue à pile ou face avec une pièce de monnaie. Connaissant les conditions initiales du lancer de la pièce, on aimerait connaître sa trajectoire.

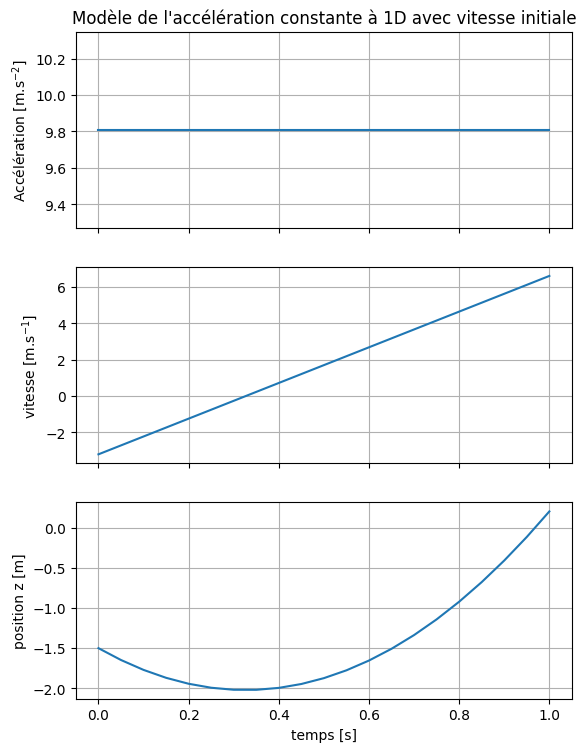
Les trois représentations du mouvement de la pièce de monnaie sont l’accélération \(a\), la vitesse \(v\) et la position \(z\) selon l’axe \(z\) :

\[\begin{split} \left\{ \begin{array}{lll} a(t) &=& g \\ v(t) &=& gt + v_0\\ z(t) &=& \dfrac{1}{2} gt^2 + v_0 t + z_0 \end{array} \right. \end{split}\]

Vous choisirez pour cet exercice de représenter numériquement les fonctions par des tableaux Numpy 1D (représentation discrète). Vous choisirez vous-même l’intervalle et le pas de temps pour la représentation discrète.

1. Représenter graphiquement, l’un au-dessous de l’autre grâce à la fonction subplot(), l’accélération, la vitesse et la position \(z\) de la pièce, pour \(v_0 = -3.2 \mathrm{~m.s^{-1}}\) et \(z_0 = -1.5 \mathrm{~m}\). Choisir l’intervalle de temps de façon à ce que la pièce dépasse de peu la position \(z=0\).

Show code cell source Hide code cell source

# Importation des modules
import numpy as np
import matplotlib.pyplot as plt

# Paramètres du problème
pesanteur = 9.81 # m.s**-2
vitesse_initiale = -3.2 # m.s**-1
position_z_initiale = -1.5 # m
temps_initial = 0 # s
temps_final = 1.0 # s
pas_temps = 0.05 # s

# Création du tableau temps (discrétisation)
intervalle = temps_final - temps_initial
num_points = int(intervalle / pas_temps) + 1   # Nombre d'éléments
temps = np.linspace(temps_initial, temps_final, num_points)

# Création des autres tableaux
acceleration = np.ones(temps.shape) * pesanteur
vitesse = pesanteur * temps + vitesse_initiale
position_z = 1 / 2 * pesanteur * temps ** 2 + vitesse_initiale * temps + position_z_initiale

# Représentation de l'accélération
plt.subplot(3, 1, 1)
plt.plot(temps, acceleration)
plt.ylabel('Accélération [m.s$^{-2}$]')
plt.grid()
plt.tick_params(axis = 'x', labelbottom = False) # Retire les labels de l'axe x
plt.title("Modèle de l'accélération constante à 1D avec vitesse initiale")

# Représentation de la vitesse
plt.subplot(3, 1, 2)
plt.plot(temps, vitesse)
plt.ylabel('vitesse [m.s$^{-1}$]')
plt.grid()
plt.tick_params(axis = 'x', labelbottom = False) # Retire les labels de l'axe x

# Représentation de la position z
plt.subplot(3, 1, 3)
plt.plot(temps, position_z)
plt.ylabel('position z [m]')
plt.xlabel('temps [s]')
plt.grid()

plt.subplots_adjust(top = 1.5) # Agrandit l'espace entre les figures

plt.show()

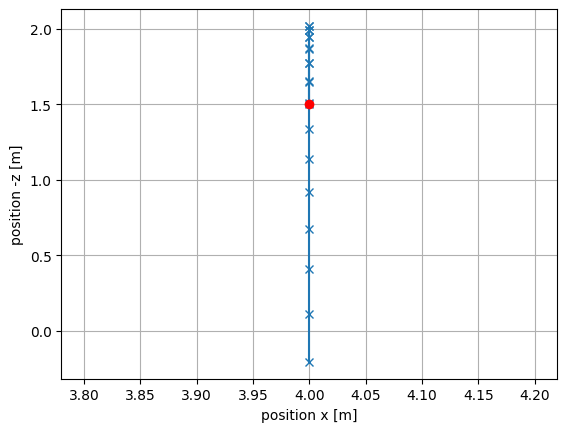
2. Représenter le mouvement de l’objet dans le plan \((x0z)\), pour \(x_0 = 4 \mathrm{~m}\). Sur cette représentation, placer un point rouge à l’endroit de la position initiale de l’objet.

Show code cell source Hide code cell source

# Paramètres du problème
position_x_initiale = 4 # m

# Création du tableau position x
position_x = np.ones(temps.shape) * position_x_initiale

# Représentation graphique du mouvement
plt.plot(position_x, -position_z, 'x-')

# Style
plt.xlabel("position x [m]")
plt.ylabel("position -z [m]")
plt.grid()

# Position initiale
plt.plot(position_x_initiale, -position_z_initiale, 'ro')

plt.show()

Tir à l’arc

Pour un tir à l’arc, nous souhaitons modéliser la trajectoire de la flèche, en utilisant le modèle de l’accélération constante. Nous modélisons la flèche par une particule ponctuelle. La cible se trouve à \(40 \mathrm{~m}\) du tireur, à une hauteur de \(1,\!5 \mathrm{~m}\), et fait \(50 \mathrm{~cm}\) de diamètre.

Pour un mouvement à 2D suivant les axes \(z\) et \(x\), nous avons les équations suivantes pour les vitesses suivant les axes \(z\) et \(x\), respectivement :

\[\begin{split} \left\{ \begin{array}{lll} v_z(t) &=& gt + v_0^z\\ v_x(t) &=& v_0^x \end{array} \right. \end{split}\]

et pour les positions suivant les axes \(z\) et \(x\), respectivement :

\[\begin{split} \left\{ \begin{array}{lll} z(t) &=& \dfrac{1}{2} gt^2 + v_0^z t + z_0\\ x(t) &=& v_0^x t + x_0 \end{array} \right. \end{split}\]

1. Créer un DataFrame Pandas pour représenter le mouvement. Vous choisirez vous-même la discrétisation des fonctions. L’index du DataFrame doit représenter le temps. Vous allez ensuite créer 5 colonnes pour le DataFrame, représentant : l’accélération, la vitesse suivant l’axe \(z\), la vitesse suivant l’axe \(x\), la position suivant l’axe \(z\), et la position suivant l’axe \(x\). Les paramètres du problème sont :

\[\begin{split} \left\{ \begin{array}{lll} v_0^z = -1.3 \ \mathrm{m.s^{-1}}\\ v_0^x = 99.6 \ \mathrm{m.s^{-1}}\\ z_0 = -1.5 \ \mathrm{m}\\ x_0 = 0.0 \ \mathrm{m} \end{array} \right. \end{split}\]

Show code cell source Hide code cell source

# Importation des modules
import numpy as np
import pandas as pd

# Paramètres du problème
pesanteur = 9.81 # m.s**-2
vitesse_z_initiale = -1.3 # m.s**-1
position_z_initiale = -1.5 # m
vitesse_x_initiale = 99.6 # m.s**-1
position_x_initiale = 0.0 # m
temps_initial = 0 # s
temps_final = 0.5 # s
pas_temps = 0.01 # s

# Création du tableau temps (discrétisation)
intervalle = temps_final - temps_initial
num_points = int(intervalle / pas_temps) + 1   # Nombre d'éléments
temps = np.linspace(temps_initial, temps_final, num_points)

# Création du DataFrame avec une colonne accélération
acceleration = np.ones(temps.shape) * pesanteur
df = pd.DataFrame(data = acceleration, index = temps, columns = ['acceleration'])

# Création des autres colonnes
df["vitesse_z"] = pesanteur * temps + vitesse_z_initiale
df["vitesse_x"] = vitesse_x_initiale
df["position_z"] = 1 / 2 * pesanteur * temps ** 2 + vitesse_z_initiale * temps + position_z_initiale
df["position_x"] = vitesse_x_initiale * temps + position_x_initiale

# Affichage du tableau pour vérification
df.head(n = 10)

	acceleration	vitesse_z	vitesse_x	position_z	position_x
0.00	9.81	-1.3000	99.6	-1.500000	0.000
0.01	9.81	-1.2019	99.6	-1.512509	0.996
0.02	9.81	-1.1038	99.6	-1.524038	1.992
0.03	9.81	-1.0057	99.6	-1.534585	2.988
0.04	9.81	-0.9076	99.6	-1.544152	3.984
0.05	9.81	-0.8095	99.6	-1.552738	4.980
0.06	9.81	-0.7114	99.6	-1.560342	5.976
0.07	9.81	-0.6133	99.6	-1.566966	6.972
0.08	9.81	-0.5152	99.6	-1.572608	7.968
0.09	9.81	-0.4171	99.6	-1.577269	8.964

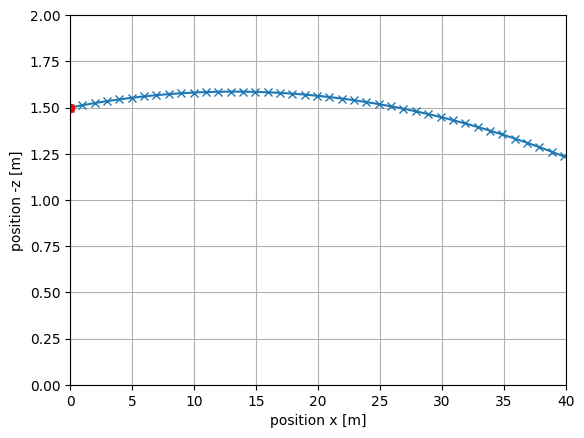
2. Représenter le mouvement de l’objet dans le plan \((x0z)\), pour \(z\in [0,2] \mathrm{~m}\) et \(x\in [0,40] \mathrm{~m}\). Sur cette représentation, placer un point rouge à l’endroit de la position initiale de l’objet.

Show code cell source Hide code cell source

# Importation des modules
import matplotlib.pyplot as plt

# Représentation graphique du mouvement
plt.plot(df["position_x"], -df["position_z"], 'x-')

# Style
plt.xlabel("position x [m]")
plt.ylabel("position -z [m]")
plt.ylim(0, 2)
plt.xlim(0, 40)
plt.grid()

# Position initiale
plt.plot(position_x_initiale, -position_z_initiale, 'ro')

plt.show()

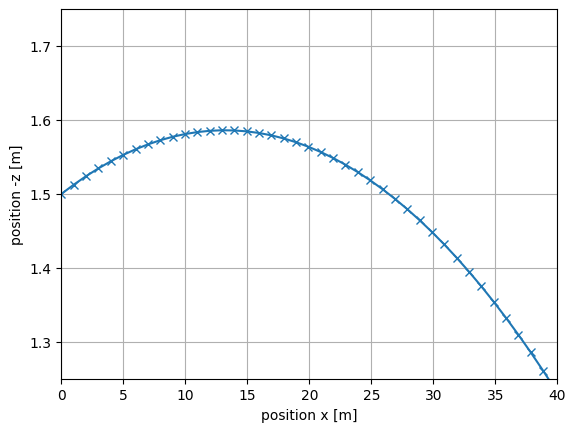
3. En choississant mieux les limites des axes pour la représentation du mouvement, déterminez si le tireur atteint la cible.

Show code cell source Hide code cell source

# Représentation graphique du mouvement
plt.plot(df["position_x"], -df["position_z"], 'x-')

# Style
plt.xlabel("position x [m]")
plt.ylabel("position -z [m]")
plt.ylim(1.5 - 0.25, 1.5 + 0.25)
plt.xlim(0,40)
plt.grid()

plt.show()

# On voit que le tireur n'atteint pas sa cible

4. En réflechissant aux limites de votre modèle, est-ce que la conclusion de cette étude pourrait être changée ? Comment améliorer le modèle ?

Le modèle de particule ponctuelle pour une flèche n’est sûrement pas adapté. En effet, la flèche, de par sa longueur et son empenage, est optimisée pour garder une trajectoire horizontale. Il faudrait adapter notre modèle de flèche pour prendre en compte son extension, et notre modèle d’interaction pour prendre en compte les frottements de l’air.