Méthodes d’Euler et de Runge-Kutta#

La tasse de café#

Lorsque la différence \(D(t)\) entre la température du café au temps \(t\) et celle de l’air ambiant n’est pas trop grande, on peut considérer qu’elle varie selon la relation :

\[ \frac{\text{d}D}{\text{d}t} = -r D(t) \]

où \(r=1/\tau\) est un paramètre positif.

  1. Résoudre cette équation avec la méthode d’Euler entre \(0\) et \(30\mathrm{~mn}\), pour la condition initiale \(D(0) = 65.3\mathrm{~°C}\) et la valeur du paramètre \(r = 0.1\mathrm{~mn^{-1}}\). On prendra un pas de \(0.5\mathrm{~mn}\).

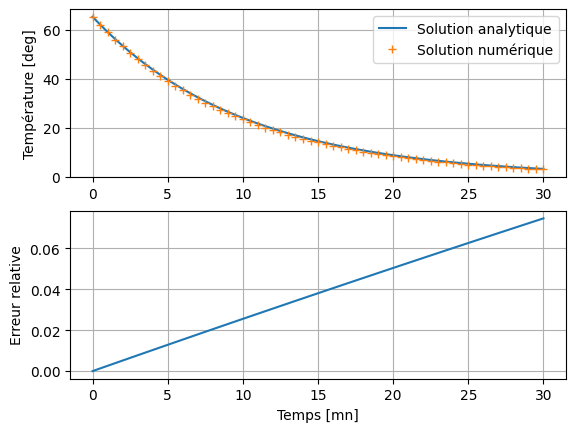
  2. Comparer graphiquement la solution numérique avec la solution analytique :

\[ D (t) = D_0 e^{-rt} \]

  1. Représenter graphiquement l’erreur relative entre les 2 méthodes

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

# Paramètres
r = 0.1 # mn^-1
ti = 0 # mn
te = 30 # mn
step = 0.5 # mn
ordre = 1

# Conditions initiales
D_ini = 65.3 # °C

# Loi de décroissance
def derivee_D (D, t):
    '''
        Loi de décroissance dD/dt = - r D
    '''
    return -r * D

# Méthode d'Euler
def Euler(start, end, step, v_ini, derivee, ordre):
    '''
        Application de la méthode d'Euler
    '''
    # Création du tableau temps
    interval = end - start                     # Intervalle
    num_points = int(interval / step) + 1      # Nombre d'éléments
    t = np.linspace(start, end, num_points)    # Tableau temps t

    # Initialisation du tableau v
    v = np.empty((ordre, num_points))

    # Condition initiale
    v[:, 0] = v_ini 

    # Boucle for
    for i in range(num_points - 1):
        v[:, i + 1] = v[:, i] + step * derivee(v[:, i], t[i])

    # Argument de sortie
    return t, v

# Méthode d'Euler
t, Deu = Euler(ti, te, step, D_ini, derivee_D, ordre)

# Solution analytique
Da = D_ini * np.exp(-r * t)

# Comparaison des solutions
plt.subplot(2, 1, 1)
plt.plot(t, Da, label = 'Solution analytique')
plt.plot(t, Deu[0, :], '+', label = 'Solution numérique')
plt.ylabel('Température [deg]')
plt.grid()
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(t, np.abs((Deu[0, :] - Da) / Da))
plt.ylabel("Erreur relative")
plt.xlabel('Temps [mn]')
plt.grid()
plt.show()
../../../_images/1524f124b5d38cc3de89247c47dfc93287ec4593e9cfefee33662229c9fac35d.png

Méthodes de Runge-Kutta#

La méthode d’Euler est simple à programmer mais est toutefois peu précise au-delà des temps courts. Il existe de nombreuses méthodes pour y remédier. Une classe de méthodes couramment utilisées est la classe des méthodes de Runge-Kutta présentées ci-dessous.

Considérons les équations différentielles ordinaires d’ordre 1 de la forme :

\[ u'(t) = F(u,t) \]

avec une condition initiale :

\[ u(0) = U_0 \]

où \(u\) est une quantité scalaire ou vectorielle.

L’intégration de l’EDO entre \(t_k\) et \(t_{k+1}= t_k+\Delta t \) donne formellement :

\[ u(t_{k+1})-u(t_k) = \int_{t_k}^{t_k+\Delta t} \, F(u(t),t)\,\text{d}t \]

Dans la méthode d’Euler explicite, l’intégrale est approximée par

\[ \int_{t_k}^{t_k+\Delta t} \, F(u(t),t)\,\text{d}t = F(u(t_k),t_k) \Delta t \]

À chaque pas l’erreur est de l’ordre de \(M(\Delta t)^2/2\) où \(M\) est l’ordre de grandeur de la dérivée de \(F\) par rapport à \(t\). Au bout de \(N\) pas d’intégration, l’erreur cumulée est donc de l’ordre de \(\Delta t\) (et on voit facilement qu’il en sera de même pour la méthode implicite). D’où la qualification de méthode d’ordre 1 en \(\Delta t\) donnée à la méthode d’Euler.

Methodes de Runge-Kutta (explicite) d’ordre 2 (méthodes RK2) :#

On peut améliorer l’estimation \(u_{k+1}\) de \(u(t_{k+1})\) en évaluant \(F\) à un point intermédiaire, par exemple le point milieu du pas d’intégration et refaire l’intégration de \(u\) à partir de \(t_k\) en utilisant cette évaluation de l’intégrande :

\[ d_1 = F(u_k, t_k) \]
\[ u_{k,1} = u(t_k)+ d_1 \frac{\Delta t}{2} \]
\[ d_2 = F\left(u_{k,1}, t_k + \frac{\Delta t}{2} \right) \]
\[ u_{k+1} = u_k + d_2 \Delta t \;. \]

D’où le nom de méthode RK2 du point milieu. On peut montrer que les erreurs cumulées sont d’ordre \(\Delta t^2\), d’où le nom de méthode de Runge-Kutta d’ordre 2.

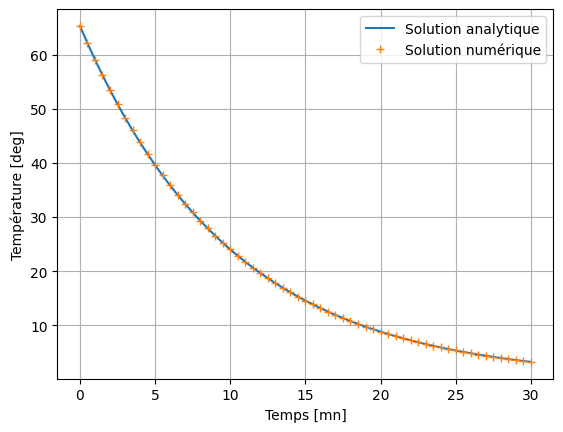
  1. Adapter le script de la méthode d’Euler ci-dessous pour appliquer la méthode RK2 et tester la méthode pour le problème du refroidissement de la tasse de café

Hide code cell source 
# Méthode d'Euler
def Euler(start, end, step, v_ini, derivee, ordre):
    '''
        Application de la méthode d'Euler
    '''
    # Création du tableau temps
    interval = end - start                     # Intervalle
    num_points = int(interval / step) + 1      # Nombre d'éléments
    t = np.linspace(start, end, num_points)    # Tableau temps t

    # Initialisation du tableau v
    v = np.empty((ordre, num_points))

    # Condition initiale
    v[:, 0] = v_ini 

    # Boucle for
    for i in range(num_points - 1):
        v[:, i + 1] = v[:, i] + step * derivee(v[:, i], t[i])

    # Argument de sortie
    return t, v
Hide code cell source 
def rk2(start, end, step, v_ini, derivee, ordre):
    '''
        Application de la méthode rk2
    '''
    # Création du tableau temps
    interval = end - start                     # Intervalle
    num_points = int(interval / step) + 1      # Nombre d'éléments
    t = np.linspace(start, end, num_points)    # Tableau temps t

    # Initialisation du tableau v
    v = np.empty((ordre, num_points))

    # Condition initiale
    v[:, 0] = v_ini 

    # Boucle for
    for i in range(num_points - 1):
        d1 = derivee(v[:, i], t[i])
        v1 = v[:, i] + step / 2 * d1
        d2 = derivee(v1, t[i] + step / 2)
        v[:, i + 1] = v1 + step / 2 * d2

    # Argument de sortie
    return t, v

# Méthode rk2
t, Drk2 = rk2(ti, te, step, D_ini, derivee_D, ordre)

# Comparaison des solutions
plt.plot(t, Da, label = 'Solution analytique')
plt.plot(t, Drk2[0, :], '+', label = 'Solution numérique')
plt.xlabel('Temps [mn]')
plt.ylabel('Température [deg]')
plt.grid()
plt.legend()
plt.show()
../../../_images/f1615150baa4fdab9449a0a204ab209e2d93617c252a7d36a52bad32d699e9c1.png

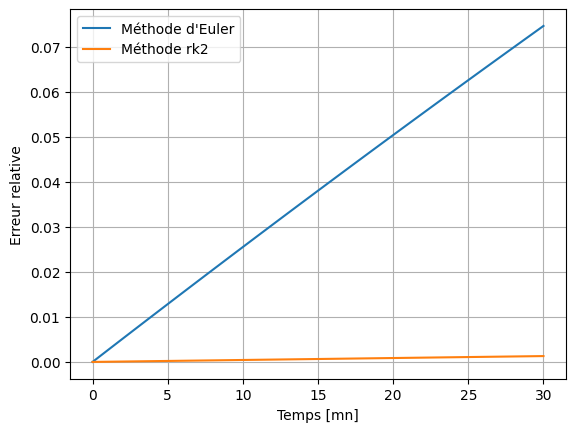
  1. Calculer l’erreur relative en fonction du temps et comparer à la méthode d’Euler

Hide code cell source 
# Comparaison des méthodes
plt.plot(t, np.abs((Deu[0, :] - Da) / Da), label = "Méthode d'Euler")
plt.plot(t, np.abs((Drk2[0, :] - Da) / Da), label = "Méthode rk2")
plt.ylabel("Erreur relative")
plt.xlabel('Temps [mn]')
plt.legend()
plt.grid()
plt.show()
../../../_images/cf192d558ab019d93142abcbc885c9e131c88f56a8259c6a35b4471b38878101.png

Methode de Runge-Kutta (explicite) d’ordre 4 (méthode RK4)#

Nous nous limiterons au schéma d’intégration suivant, couramment utilisé, basé sur une estimation de l’intégrale par la méthode de Simpson :

\[ d_1 = F\left(t_k , u_{k} \right) \]
\[ d_2 = F\left(t_k + \frac{\Delta t}{2} , u_{k} + \frac{\Delta t}{2} d_1 \right) \]
\[ d_3 = F\left(t_k + \frac{\Delta t}{2} , u_{k} + \frac{\Delta t}{2} d_2 \right) \]
\[ d_4 = F\left(t_k + \Delta t , u_{k} + \Delta t d_3\right) \]
\[ u_{k+1} = u_k + \frac{\Delta t}{6} \left[ d_1+ 2 d_2 + 2 d_3 + d_4 \right] \]

où l’erreur par pas est d’ordre \(\Delta t^5\) et l’erreur cumulée est d’ordre \(\Delta t^4\).

  1. Adapter la fonction de la méthode d’Euler de l’exercice précédent pour appliquer la méthode RK4, et tester la méthode pour le problème du refroidissement de la tasse de café

Hide code cell source 
# Méthode rk4
def rk4(start, end, step, v_ini, derivee, ordre):
    '''
        Application de la méthode rk4
    '''
    # Création du tableau temps
    interval = end - start                     # Intervalle
    num_points = int(interval / step) + 1      # Nombre d'éléments
    t = np.linspace(start, end, num_points)    # Tableau temps t

    # Initialisation du tableau v
    v = np.empty((ordre, num_points))

    # Condition initiale
    v[:, 0] = v_ini 

    # Boucle for
    for i in range(num_points - 1):
        d1 = derivee(v[:, i], t[i])
        d2 = derivee(v[:, i] + step / 2 * d1, t[i] + step / 2)
        d3 = derivee(v[:, i] + step / 2 * d2, t[i] + step / 2)
        d4 = derivee(v[:, i] + step * d3, t[i] + step)
        v[:, i + 1] = v[:, i] + step / 6 * (d1 + 2 * d2 + 2 * d3 + d4)

    # Argument de sortie
    return t, v

# Méthode rk4
t, Drk4 = rk4(ti, te, 0.5, D_ini, derivee_D, ordre)

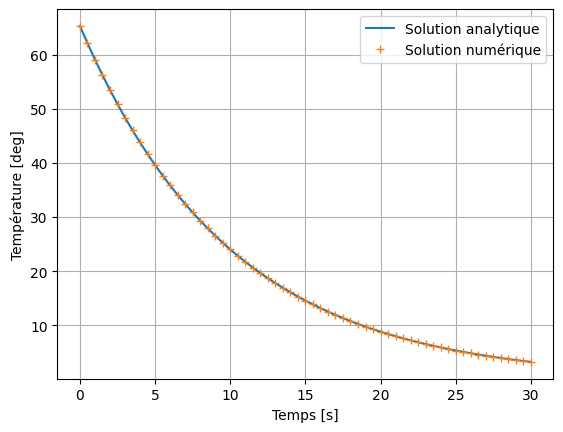
# Comparaison des solutions
plt.plot(t, Da, label = 'Solution analytique')
plt.plot(t, Drk4[0, :], '+', label = 'Solution numérique')
plt.xlabel('Temps [s]')
plt.ylabel('Température [deg]')
plt.grid()
plt.legend()
plt.show()
../../../_images/76f7d46bbde893d3141b8656a29ab9d68b63eee0c02cfa96964bfeb37c275e63.png

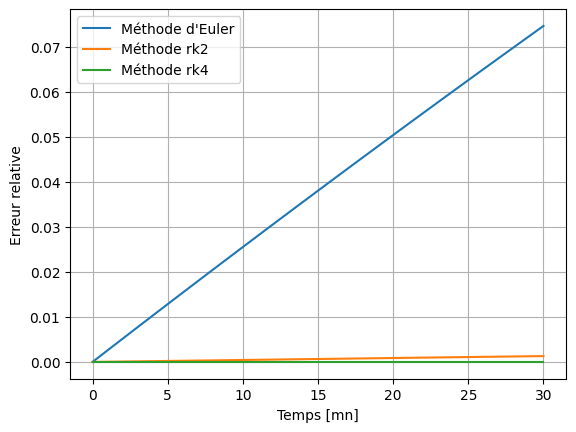
  1. Calculer l’erreur relative en fonction du temps et comparer à la méthode d’Euler et à RK2

Hide code cell source 
# Comparaison des méthodes
plt.plot(t, np.abs((Deu[0, :] - Da) / Da), label = "Méthode d'Euler")
plt.plot(t, np.abs((Drk2[0, :] - Da) / Da), label = "Méthode rk2")
plt.plot(t, np.abs((Drk4[0, :] - Da) / Da), label = "Méthode rk4")
plt.ylabel("Erreur relative")
plt.xlabel('Temps [mn]')
plt.legend()
plt.grid()
plt.show()
../../../_images/26d1b9c15d5dacf924c4c72517d018f26288d093162830399e1e1f1f8b8dd232.png